thomas
deckker
architect
critical reflections

Thoughts on Making: Stereotomy at Besançon
2025
2025

Amédée-François Frézier: La Théorie et la Pratique de la Coupe des Pierres (Strasbourg and Paris 1737) Book 1 Plate 1
Circles, ellipses, parabolas and hyperbolas can all be derived from cones, hence this type of geometry is known as conics. This was known in Antiquity by mathematicians such as Apollonius of Perga.
Thoughts on Making: Stereotomy at Besançon
The art and science of stereotomy can be seen as the fulcrum between the worlds of the architect - civil or military - and the mason. For the architect it was the practical end of an abstract geometry which encompassed buildings and landscapes; for the mason the theoretical end of the labour of cutting stone.

Amédée-François Frézier: La Théorie et la Pratique de la Coupe des Pierres (Strasbourg and Paris 1737) Book 1 Frontispiece
From Vitruvius Book 1 Chapter 1: Geometry is of great use to architecture, and teaches the use of the ruler and compass (which chiefly facilitates the delineation of the plans of buildings) and the management of squares, levels, and lines.
[1]
Stereotomy is the cutting of stones in three dimensions based on drawings of the design in two dimensions, to enable stones to be cut in a yard and then placed on site where cutting would be time-consuming and dangerous. The link between two and three dimensions was geometry, particularly descriptive geometry - the translation between two and three dimensions, and projective geometry - the translation of one shape on to another, which, in stereotomy, means complex shapes like splayed vaults. Beyond this practical requirement we may see an enjoyment of geometry for its own sake, especially in ornamental staircases and elaborate vaults. The cutting of stone obviously was an esoteric skill of masons, part of their guild knowledge [2], but in the renaissance both architecture and masonry became the subjects of discourses open to all educated people.

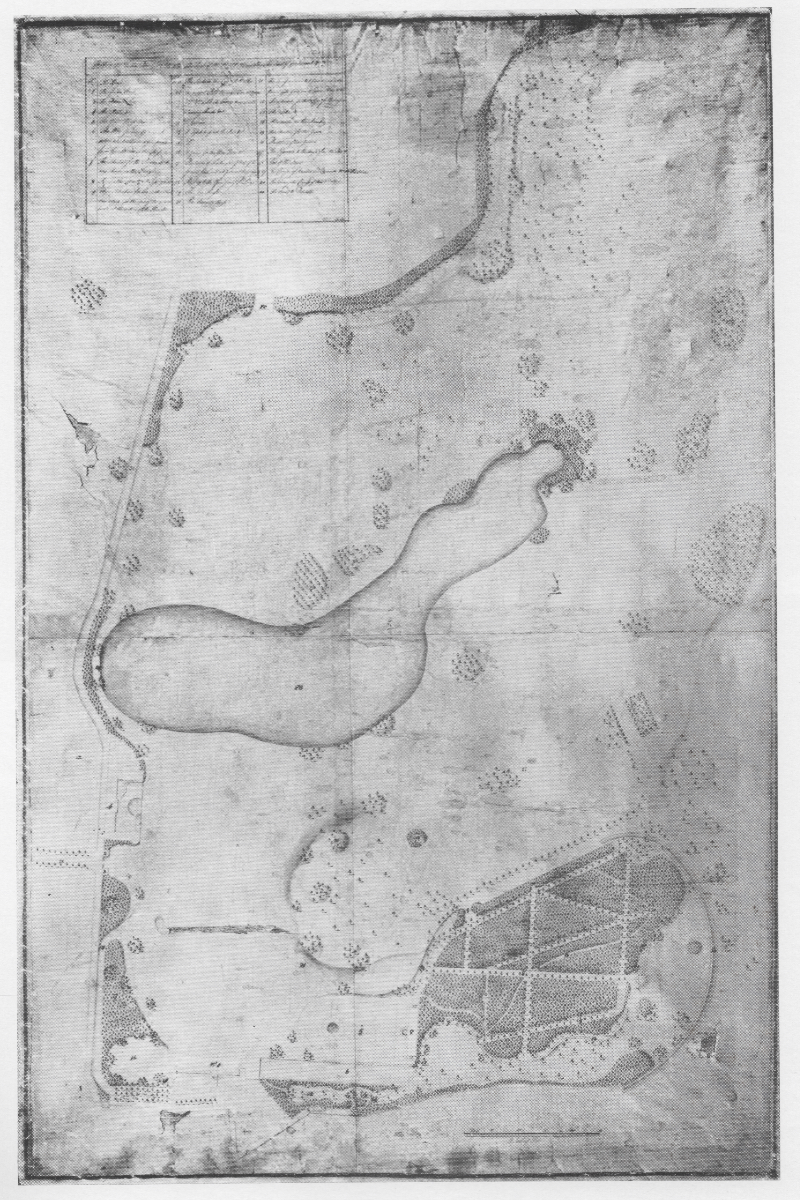
Plans de Besançon et de ses travaux de défense par Vauban, en 1714 Frontispiece
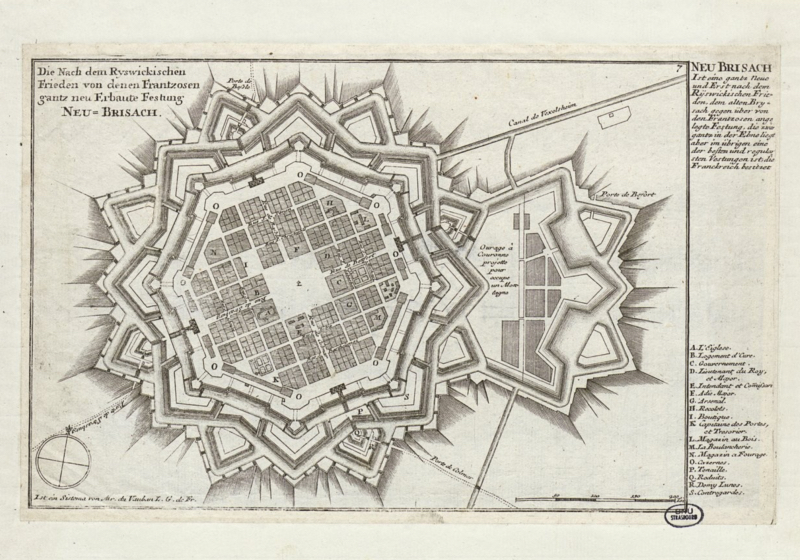
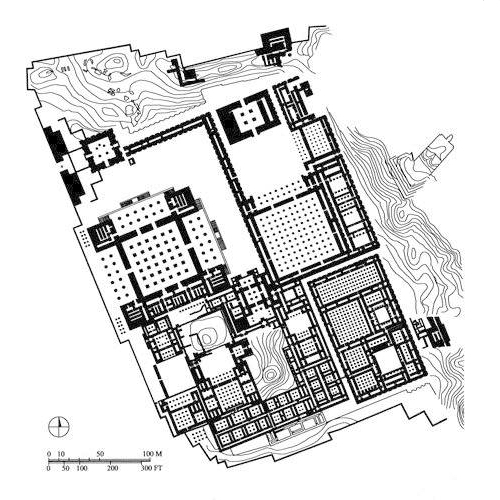
The Vauban Citadelle at Besançon (1668-1711) may be considered a textbook illustration of stereotomy. It is one of twelve groups of fortifications by the French military engineer Sébastien Le Prestre de Vauban rightly listed as a World Heritage Site by UNESCO.[3] These fortifications formed a defensive ring around France and exhibited designs adapted to flat plains, such as Neuf-Brisach, where manipulation of landscape was part of the architectural strategy, or mountainous terrain such as Besançon, almost impregnable by itself.

Vauban: The Citadelle, Besançon
photo Thomas Deckker 2024
photo Thomas Deckker 2024
Frézier: The Theory and Practice of Stereotomy
The reason that the Vauban Citadelle at Besançon may be considered a textbook illustration of stereotomy is because stone cut to form vaults and embrasures may be seen everywhere and these obviously follow textbooks of stereotomy such as Amédée-François Frézier's La Théorie et la Pratique de la Coupe des Pierres (Strasbourg and Paris 1737). This particular textbook was not published until after Vauban's death, but it follows a development of textbooks of stereotomy contemporaneous with those on renaissance buildings themselves. We can be sure it was intended to be of practical use: it was dedicated to the marquis d'Asfeld, director-general of fortifications in France.

Frézier: La Théorie et la Pratique de la Coupe des Pierres Book 1 Plate 21
A large embrasure splayed at an angle to the wall.
A large embrasure splayed at an angle to the wall.

Vauban: The Citadelle, Besançon
photo Thomas Deckker 2024
photo Thomas Deckker 2024

Frézier: La Théorie et la Pratique de la Coupe des Pierres Book 2 Plate 45
A complex embrasure in a flank wall of a bastion. Note the double splay in the embrasure, opening to both the interior and exterior face of the wall in illustration 112 in the adjacent plate.
A complex embrasure in a flank wall of a bastion. Note the double splay in the embrasure, opening to both the interior and exterior face of the wall in illustration 112 in the adjacent plate.

Vauban: The Citadelle, Besançon
photo Thomas Deckker 2024
photo Thomas Deckker 2024

Frézier: La Théorie et la Pratique de la Coupe des Pierres Book 2 Plate 61
Frézier notes in the text that this oblique vault, whose beds do not align to the axis must be considered as a section of a scalene cylinder, or a cylinder leaning over at an angle resulting in an ellipse in plan. This may be seen in illustration 15 at the bottom left of Book 1 Plate 1 at the top of this page.
Frézier notes in the text that this oblique vault, whose beds do not align to the axis must be considered as a section of a scalene cylinder, or a cylinder leaning over at an angle resulting in an ellipse in plan. This may be seen in illustration 15 at the bottom left of Book 1 Plate 1 at the top of this page.

Vauban: The Citadelle, Besançon
photo Thomas Deckker 2024
photo Thomas Deckker 2024

Frézier: La Théorie et la Pratique de la Coupe des Pierres Book 2 Plate 33
Note the asymmetrical vault described by Frézier as a hyperbolic spiral, a spiral first identified by the French mathematician Pierre Varignon in 1704 (illustration 52 in the adjacent plate). This was one of several ways shown of forming a vault such as a semicircle, an ellipse (illustration 49), and a cycloid (illustration 51). Neither the hyperbolic spiral, cycloid nor volute are conic sections but they share a similar mathematical basis. Incidentally, the architect Louis Kahn, an admirer of stereotomy, used cycloidal vaults at the Kimbell Art Museum. [4]
Note the asymmetrical vault described by Frézier as a hyperbolic spiral, a spiral first identified by the French mathematician Pierre Varignon in 1704 (illustration 52 in the adjacent plate). This was one of several ways shown of forming a vault such as a semicircle, an ellipse (illustration 49), and a cycloid (illustration 51). Neither the hyperbolic spiral, cycloid nor volute are conic sections but they share a similar mathematical basis. Incidentally, the architect Louis Kahn, an admirer of stereotomy, used cycloidal vaults at the Kimbell Art Museum. [4]

Vauban: The Citadelle, Besançon
photo Thomas Deckker 2024
photo Thomas Deckker 2024
Something perhaps not Frézier
I did come across some curious features in the Citadelle: what could only be called fan vaults in some passageways. It may be they were rounded as a practical gesture, to reduce damage, or it may be these represented a continuation of masons' detailing where they would not interfere with the operation of the fortress. Fan vaults were one of the great achievements of masons' architecture during the Gothic period in England, culminating in King's College Chapel, Cambridge (1446-1515). French Gothic masons, on the other hand, almost always used quadripartite groin vaults, formed by the intersection of two ribbed vaults.

Frézier: La Théorie et la Pratique de la Coupe des Pierres Book 2 Plate 60
A groin vault was assumed to be concave rather than convex. Compare illustration 211 in the adjacent plate to what may be observed on site below.
A groin vault was assumed to be concave rather than convex. Compare illustration 211 in the adjacent plate to what may be observed on site below.


Vauban: The Citadelle, Besançon
photo Thomas Deckker 2024
photo Thomas Deckker 2024
Note the curvature of the groin vault is positive rather than negative. In classical architecture a groin vault would be concave, formed by the intersection of 2 tunnel vaults. The fan vault, normally associated with English Gothic architecture is convex and its appearance here is unusual.

Norwich Cathedral
photo Thomas Deckker 1988
photo Thomas Deckker 1988
Norwich Cathedral, with a Gothic lierne vault (c. 1446-72) over a Norman, or Romanesque, arcade, triforium and clerestory. Romanesque architecture was a distant memory of classical architecture, but Gothic masons were not interested in that aesthetic world at all. This lierne vault is a predecessor, structurally almost identical, of the fan vault.
Descriptive and Projective Geometry
Projective geometry had several immediate applications for Vauban. It could be used to predict the flight of artillery shells, in offence or defence. As a result it could be used to define the geometry of fortifications to counter them or project them. Projective geometry was the foundation of optics so had practical applications in the newly founded telescopes and microscopes. These could be used for accurate surveying - telescopes for long distances and microscopes for vernier scales. And of course it formed the basis of stereotomy.
The first known French treatise on stereotomy was Le premier tome de l'architecture (1567) by Philibert de l'Orme, whose work may be seen at the Château de Chenonceau (1555). There was a revolution in descriptive and projective geometry in the early 17th century which dramatically improved the precision, and increased the scope, of stereotomy as may be seen in later works.

Philibert de l'Orme: Le premier tome de l'architecture Plate 77
A simple embrasure on the corner of a bastion.
Compare this to the later illustration in Frézier's La Théorie et la Pratique de la Coupe des Pierres.
A simple embrasure on the corner of a bastion.
Compare this to the later illustration in Frézier's La Théorie et la Pratique de la Coupe des Pierres.

Philibert de l'Orme: Château de Chenonceau 1555
photo Thomas Deckker 1984
photo Thomas Deckker 1984
Note the pendant bosses in the vaulted ceiling. These are usually associated with English Gothic architecture and may be a hangover from Gothic masonry practices. The fan vaults in the Citadelle at Besançon may be their distant descendent. Ceilings of this type were exorcised from the later, stricter, application of classical architecture but pendant bosses (in wood) were actually illustrated by de l'Orme in plate 111 of Le premier tome de l'architecture.

Girard Desargues: Universal method of Mr Desargues, of practicing perspective by geometrical figures
The first known geometrical solution to relating all 3 axes - height, width and depth - of perspective to 2 dimensional drawings. Previously depth in perspective had been derived empirically.
The first known geometrical solution to relating all 3 axes - height, width and depth - of perspective to 2 dimensional drawings. Previously depth in perspective had been derived empirically.
Girard Desargues, a mathematician and architect, wrote treatises on descriptive geometry, projective geometry, and conics: Manière universelle de Mr Desargues, pour pratiquer la perspective par petit-pied, comme le géométral [Universal method of Mr Desargues, of practicing perspective by geometrical figures] (Paris 1647) and Brouillon project d'une atteinte aux événements des rencontres du Cône avec un Plan [Rough draft for an essay on the results of taking plane sections of a cone] (Paris 1648), regarded as the foundation of projective geometry.

Girard Desargues: La pratique du trait a preuves de Mr. Desargues lyonnois pour la coupe des pierres en l'architecture
This plate conveniently shows the cut blocks, the mason's tools for shaping and setting out, and the geometrical abstraction which allowed the stone to be cut in a yard and fitted into place in the vault without further time-consuming and dangerous work at height.
This plate conveniently shows the cut blocks, the mason's tools for shaping and setting out, and the geometrical abstraction which allowed the stone to be cut in a yard and fitted into place in the vault without further time-consuming and dangerous work at height.
Desargues was also a practicing architect: he published a work on stereotomy - La pratique du trait a preuves de Mr. Desargues lyonnois pour la coupe des pierres en l'architecture [The practical treatise of Mr. Desargues, of Lyon, on the cutting of stone in architecture] (1643) and designed the Hôtel Roland (c. 1648) in Paris, with an oval vestibule and unusual diagonal staircase.[5] This was considered important enough at the time to be illustrated in two major catalogues of French architecture, the Petit Marot in 1654 and the Grand Marot in 1670.

Girard Desargues: Hôtel Roland, Paris from Jacques Androuet du Cerceau: Petit Œuvre d'Architecture de Jean Marot (Paris 1654)
It is a strange feature of the architecture of the renaissance that some mathematicians could become celebrated architects apparently out of nowhere - Christopher Wren (St. Paul's Cathedral, London, 1669-1708) and Claude Perrault (the East Front of the Louvre, Paris, 1667-74), for example. Doubtless their knowledge of stereotomy allowed them to communicate with masons. Masons did not have the education to design large complex buildings but several celebrated architects started the careers as masons - Philibert de l'Orme, Andrea Palladio and Nicholas Hawksmoor, for example. Doubtless their training in stereotomy gave them a substantial basis for practicing architecture.

Philibert de l'Orme: Le premier tome de l'architecture no plate number
One of the more abstract drawings from Le premier tome de l'architecture showing the setting out of an Ionic volute. Compare this volute to the asymmetrical vault in illustration 52 in Book 2 Plate 33 of La Théorie et la Pratique de la Coupe des Pierres above. This plate shows the approximation of a volute set out with compasses, in much the same way as the Serlian oval was an approximation of an ellipse (shown in Book 1 of his Il Primo libro d'architettura, published in Paris in 1545).
One of the more abstract drawings from Le premier tome de l'architecture showing the setting out of an Ionic volute. Compare this volute to the asymmetrical vault in illustration 52 in Book 2 Plate 33 of La Théorie et la Pratique de la Coupe des Pierres above. This plate shows the approximation of a volute set out with compasses, in much the same way as the Serlian oval was an approximation of an ellipse (shown in Book 1 of his Il Primo libro d'architettura, published in Paris in 1545).
The practical applications of projective and descriptive geometry were obvious. They enabled the relationship between drawing and reality. There was another connection however: de l'Orme's Le premier tome de l'architecture and Frézier's La Théorie et la Pratique de la Coupe des Pierres moved between highly abstract geometrical concepts, stereotomy and the Orders of classical architecture. They seemed to belong to the same intellectual world of architecture. Why the academic world of conics, the practical world of the cutting of stone, and the aesthetic world of the Orders should be linked so closely now seems obscure and evidence of the distance between their world and ours. One thing that linked them was disciplined drawing in 2 and 3 dimensions, and that loss was serious.
Footnotes
1. Translation by William Newton, from The architecture of M. Vitruvius Pollio (London 1791), the first translation from the original Latin into English. Newton, a competent architect, rendered Vitruvius's description of Roman masons' tools into clear and comprehensible English. Some academics, perhaps unfamiliar with building sites, have made some bizarre translations. A carving of a Roman mason's tools is preserved on a funerary monument now in the Nelson-Atkins Museum of Art, Kansas City, Missouri. These include a ruler, a pair of compasses, a level and a plumb bob. The carving of the square is damaged but the instrument is identifiable. Thanks to Neil Bingham for pointing this out.
↩
2. For an analysis of medieval masonry practice see Tracing the Past, an ongoing research project at the University of Liverpool into the design and construction of vaults in England during the Middle Ages. Although obviously written from an academic perspective it is comprehensive and accessible. Among many relevant observations is an analysis of the fifteenth-century tracing floor at Wells Cathedral, an extremely rare survival in European architecture.
↩
3. Inscribed as 1283 for, among other criteria, "a work of the mind applied to military strategy, architecture and construction, civil engineering, and economic and social organisation".↩
4. This plate refers in part to mechanics, or forces transmitted from face to face of the voussoirs so that the arch is stable. For this reason each springing of the arch in illustration 52 is shown flat. This is not a feature of the hyperbolic spiral but of the logarithmic spiral, so Frézier was incorrect. However there was no way of making a distinction between a hyperbolic spiral, logarithmic spiral and volute on site so the curve would have been approximated with compasses, as Serlio describes in Book 4 and Philibert de l'Orme in the illustration above. Both the ellipse and volute may be set out with string, but approximating them with compasses was more practical.↩
5. Anthony Blunt: Art and Architecture in France 1500-1700 p. 238. ↩